
"What are we doing to help kids achieve?"
The concept of the mole has always been a challenging topic for myself and my students. The challenge comes in part when we try to imagine 6.02 x 1023 of anything. Another challenge for some students is the math and theory behind this number and concept.
Years ago I started using and tweaking an activity found in an old version of Zumdahl’s “World of Chemistry” textbook. Students start with four different type of beans. They count 50 of each bean and find the mass of each set. Students use the mass of 50 of the smallest bean and divide all of the other masses by this number. They then get the “relative” masses compared to the smallest bean. Some sample data is shown in Table 1.
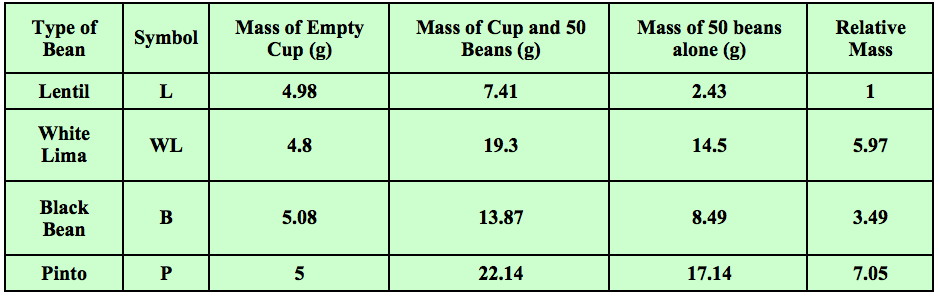
Table 1 - Students find the masses and relative masses of sets of 50 beans of four different types.
In the above example, 50 lentils had a mass of 2.43 grams. Fifty white limas had a mass of 14.5 grams. 14.5 grams divided by 2.43 grams is 5.97. This is the “relative” mass of the white limas as compared to the lentils. The relative masses of the other beans were calculated in the same manner. They were all compared to the lentils. Students had just done an activity prior to this in which the examined data that showed that as long as you are comparing the same number of items, you are also comparing the same mass ratios.
Here is where I “tweaked” the published activity. My students were instructed to carefully place on a scale for each bean an amount of beans that would get them to the relative mass for that bean. As an example, they had to place an amount of lentils on the scale to get to one gram. They then had to place white limas on the scale to get to 5.97 grams. They would repeat this for the pintos and black beans. Now the emphasis was on a simple question. Will the number of beans in the end for each relative mass in grams (which by the way was given the unit "a pot") be the same or different for all the beans? You can see some sample data in Table 2.

Table 2 - Finding the number of beans with a mass equal to the relative mass of each type of bean.
In the end, students saw that the same number of beans would provide the same ratio of masses of beans (Table 1). The opposite is also true. The relative mass of the beans in grams would provide the same numbers of beans which is about 20 (Data Table 2). If they did not want to count out a bunch of beans, they could just count by using the relative masses and a scale. This provided a great model for the mole. It took awhile but it was an easy transition from the relative masses of atoms and amu's to molar mass and the mole.
Moles seem to be tough for students and teachers. Do you have a great mole activity? Please share….would love to take a look.